Moar Math!
jongman@gmail.com
Will be covering...
- kcm이 어려운 거 하고 남은 쉬운 주제들
- Solving recurrences
- Inclusion-Exclusion principle
- Sprague-Grundy theorem
- Linearity of expectation
- Newton-Raphson method
- Adaptive Simpson integration
- Polynomial multiplication
Solving Recurrences
- 대원칙: 답의 형태를 찍어서 대입해서 푼다
- 2차 선형동차 점화식
- $a_{k} = \alpha \cdot a_{k-1} + \beta \cdot a_{k-2}$
- Let $a_k = r^k$ for a constant $r$, substitute and solve for $r$
- Multiple $r$: $a\cdot r_1^n + b\cdot r_2^n$도 해가 된다 (당연)
- Multiplicity: $r_1^n, n\cdot r^n, \cdots$가 해가 된다
- Boundary value: 초기값을 만족하도록 계수를 선택
- 비동차 점화식
Inclusion-Exclusion principle
- 원칙은 간단: $n$개 합집합의 크기를 구한다
- $n$개의 각 집합의 크기를 모두 더한다
- $\left(n \atop 2 \right)$개의 집합 쌍에 대해 공집합의 크기를 뺀다
- $\left(n \atop 3 \right)$개의 집합 triplet에 대해 공집합의 크기를 더한다
- ...
- 집합을 어떻게 나누느냐에 따라 크게 달라질 수 있음
Example: Derangement
- $n$개의 원소를 섞되, 그 중 아무것도 원래 위치에 있지 않은 경우의 수는?
- 어떻게 쪼개면 좋을까요?
- $A_i$ = $i$가 제 자리로 간 순열의 집합
- 답 = $n! - \left | \cup_i A_i \right |$
- By symmetry, 어떤 k개의 집합을 골라도 공집합의 크기/갯수는 같다: $(n-k)!, \left( n \atop k \right)$
- $n! - \sum_{i=0}^{n}(-1)^{n-i}\left(n \atop i \right)i!$
Example: SPOJ DOMINO2
- $n \times m$ 크기의 판을 $1 \times 2$ 크기의 도미노로 덮는 경우의 수?
- 인접한 두 가로줄에 대해 이 둘을 모두 덮는 도미노가 최소 한 개 있어야 한다
- (세로줄에 대해서도 마찬가지)
Sprague-Grundy theorem
- Game of NIM
- 모든 impartial, normal play 게임은 NIM으로 바꿀 수 있다.
- 규칙
- 게임은 한 개 이상의 서브게임으로 나누어짐
- 서브게임은 상태들의 DAG
- 매 턴 서브게임 하나를 골라 인접한 정점으로 현재 상태를 움직인다
- 더 이상 못 움직이면 진다
Sprague-Grundy (cont.)
- Grundy number
- 하나의 서브게임만 있다고 가정:
- 지는 상태(마지막 상태)의 수는 0
- 그 외의 상태에서는 이 상태에서 나가는 수들의 Grundy 수를 모은 뒤, MEX (minimum excluded number)
- 여러 개의 서브게임이 있다면:
- 각 서브게임의 상태를 XOR한다.
- 하나의 서브게임만 있다고 가정:
Sprague-Grundy 써먹기
- NIM 게임으로의 reduction이 중요!
- Kruskal (IPSC 2006)
- 최대 K개까지 가져갈 수 있다
- 한 개의 무더기라도 개수가 소수가 되면 이긴다!
- Treblecross (uva 10561)
- N개의 일렬로 된 칸이 있고, 번갈아가며 X를 놓는다
- X를 세개 연속으로 놓는 사람이 이긴다
Linearity of expectation
- 기대값의 정의: $\mathrm{E}(f(x)) = \sum_i p_i f(x_i)$
- 따라서:
- $\mathrm{E}(f(x) + g(x))$
- $= \sum_i p_i (f(x_i) + g(x_i))$
- $= \sum_i p_i f(x_i) + \sum_i p_i g(x_i)$
- $= \mathrm{E}(f(x)) + \mathrm{E}(g(x))$
- $f$와 $g$가 서로 관련있는 함수여도 상관없이 풀 수 있다
Examples
- 25명이 모자를 쓰고 있다가 다 벗어서 랜덤 셔플하고 다시 씀. 한 명이 자기 모자를 쓸 때마다 $5를 받는다. 받는 상금의 기대치는?
- $N+1$층 건물에 있는 엘리베이터에 1층에서 $K$명이 탔다. 엘리베이터가 서는 횟수의 기대치는?
- Convex Hull 넓이의 기대값
- 넓이는 기본적으로 선분별 외적값의 합
- 각 선분이 껍질에 포함될 확률로 외적값 선형결합
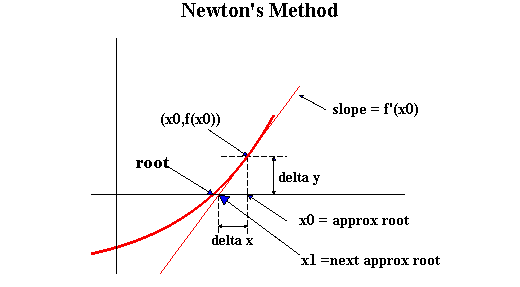
Newton-Raphson
- $f$, $f'$가 주어질 때 $f(x) = 0$의 근을 찾는다
Simpson Rule
- 사다리꼴 공식: 1차식으로 근사해 적분
- 심슨 룰: $f(x)$를 2차식으로 근사해 적분 (2차식 이하면 정확하다!)
$\int_a^b f(x) dx = \frac{b-a}{6} \left [ f(a) + 4f\left(\frac{a+b}{2}\right) + f(b) \right]$
Adaptive Simpson Rule
- 적응형 심슨 룰
- 혹시 부정확하면 구간을 더 나누자!
- 해당 구간을 절반으로 나눠 각각 심슨 룰을 붙여 보고, 전체 심슨 룰과 비교
Polynomial multiplcation
- 사실 큰 정수 곱셈과 같은 문제
- 좀 더 넓게는: Discrete Convolution
- $(f \ast g)[n] = \sum f[n-i] \cdot g[i]$
- Naive method: $O(n^2)$
- Karatsuba
- FFT
Karatsuba's big integer multiplication
- $A$, $B$가 각각 $2^{2n}$ 길이의 이진수라고 하자
- 분할!
- $A = a_{1} \cdot 2^n + a_{0}$
- $B = b_{1} \cdot 2^n + b_{0}$
- $A\cdot B = a_{1} b_{1} \cdot 2^{2n} + (a_{1}b_{0} + a_0b_1) \cdot 2^n + a_0b_0$
Karatsuba (cont.)
- 정복!
- $z_0 = a_0 \cdot b_0$
- $z_2 = a_1 \cdot b_1$
- $z_1 = (a_0 + a_1) \cdot (b_0 + b_1) - z_0 - z_1 = a_0 b_1 + a_1 b_0$
- $2^n$으로의 곱셈(shift)는 선형시간!
- 크기 $2^{2n}$인 문제를 크기 $2^n$인 문제 세개로 나눠 푼다!
FFT
- 다항식의 표현
- 계수 표현: 계수의 배열
- 포인트-값 표현: (x, y)쌍의 배열
- $(x_0, f(x_0)), (x_1, f(x_1)), \cdots$
- 두 표현은 동등하다
- $(x, y)$ 쌍이 두 개 있으면 1차식을 유일하게 정의
- 점이 3개 있으면 2차식을 유일하게 정의
FFT
- 포인트-값 표현의 장점:
- 다항식 곱셈이 선형시간에 된다!
- $(f\cdot g)(x_i) = f(x_i) g(x_i)$
- FFT의 요점
- 계수 표현을 포인트-값 표현으로 바꿔서 곱하고 다시 돌려놓자!
표현간의 변환
- 계수 표현 => 포인트-값 표현
- Horner's rule ($O(n)$)
- 단 $n+1$개의 숫자에 대해 계산해야 하므로 사실상 $O(n^2)$
- 포인트-값 표현 => 계수 표현
- $\sum_i a_i x^i_k = y_k$ 형태의 선형 시스템
선형 시스템 풀기
\(
\begin{bmatrix}
x^n_0 & x^{n-1}_0 & \cdots & x^{0}_0 \\
x^n_1 & x^{n-1}_1 & \cdots & x^{0}_1 \\
x^n_2 & x^{n-1}_2 & \cdots & x^{0}_2 \\
x^n_3 & x^{n-1}_3 & \cdots & x^{0}_3 \\
\vdots & \vdots & \vdots & \vdots
\end{bmatrix}
\cdot
\begin{bmatrix}
a_n \\
a_{n-1} \\
a_{n-2} \\
\vdots
\end{bmatrix}
=
\begin{bmatrix}
y_0 \\
y_1 \\
y_2 \\
\vdots
\end{bmatrix}
\)
시간 복잡도
- Horner rule로 변환하기 $O(n^2)$
- 포인트-값 형태에서의 곱셈 $O(n)$
- $A$의 역행렬 구하기 $O(n^3)$
- $A$와 행렬곱 $O(n^2)$
야! 신난다~
FFT
- $x_i$를 영리하게 골라서 변환 과정을 $O(n \lg n)$에 하자

$x_i$ 고르기
- Primitive root of unity: $w^n = 1$
- $w^0, w^1, w^2, \cdots$에서 다항식의 값을 계산해 둔다
- 두 가지 선택
- 복소평면: $e^{2\pi/n}$
- 모듈라 연산: $w^n = 1$ ($\mathrm{mod }K$) 인 $w, K$를 잘 찾는다
- kcm님이 가로되, "그냥 복소수 써도 된다!"
Complex primitive root of unity
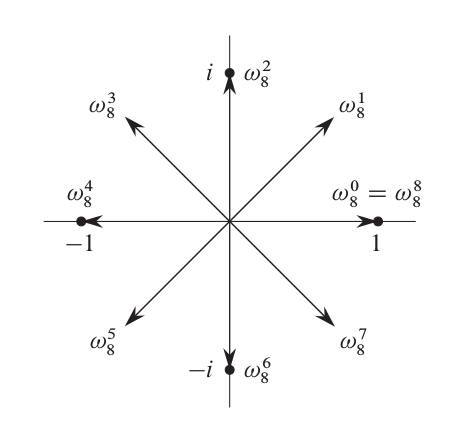
- note: $(w^i)^2 = (w^{i+n/2})^2$
DFT for root of unity $w$
- 다항식 $P$의 계수 $p_i$가 주어지고 $w$가 주어질 때:
- $1, P(w^1), P(w^2), \cdots, P(w^{n-1})$을 계산하자
- $P(x_i) = p_0 + p_1 x_i + p_2 x_i^2 + \cdots$ 를 계산하려고 한다
- $x_i = w^{i}$
분할정복!
- $P(x_i) = P_{even}(x_i) + x\cdot P_{odd}(x_i)$
- where
- $P_{even}(x_i) = p_0 + p_2 x_i + p_4 x_i^2 + \cdots + p_{n-2}x_i^{n/2}$
- $P_{odd}(x_i) = p_1 + p_3 x_i + p_5 x_i^2 + \cdots + p_{n-1}x_i^{n/2}$
- 이 때 $P_{even}(x_i^2)$와 $P_{odd}(x_i^2)$는 각각 원래 문제와 같다!
- $P(x_i) = P_{even}(x_i^2) + x_i P_{odd}(x_i^2)$
우왕ㅋ굳ㅋ 하려 했지만..
- 잠깐: 식의 길이는 $n/2$로 줄었지만, 변수의 수는 $n$개 그대로다!
- Root of unity의 성질에 따라
- $a = w^i$, $b = w^{i+n/2}$라고 할 때 $a^2 = b^2$
- 따라서
- $P_{even}(x_i^2)$, $P_{odd}(x_i^2)$만 있어도 $P(x_{i+n/2})$를 계산할 수 있다!
- $P(x_{i+n/2}) = P_{even}(x_i^2) + x_i \cdot w_i^{n/2} P_{odd}(x_i^2)$
결과적으로
- $n/2$ 크기의 문제 두 개로 줄어들었다! 그래서 머지를 적절히 잘 하면 $O(n \lg n)$
역변환
- 역시 Root of unity의 성질로부터 역행렬의 구조가 정해진다
- $A_jk = \frac{w^{-jk}}{n}$
- 그래서 싸바싸바하면 결과적으로: $w^{n-1}$에 대해 DFT를 계산하면 된다!
- (이쯤 되면 그냥 믿고 싶다!)
구현을 보자!
감사합니당